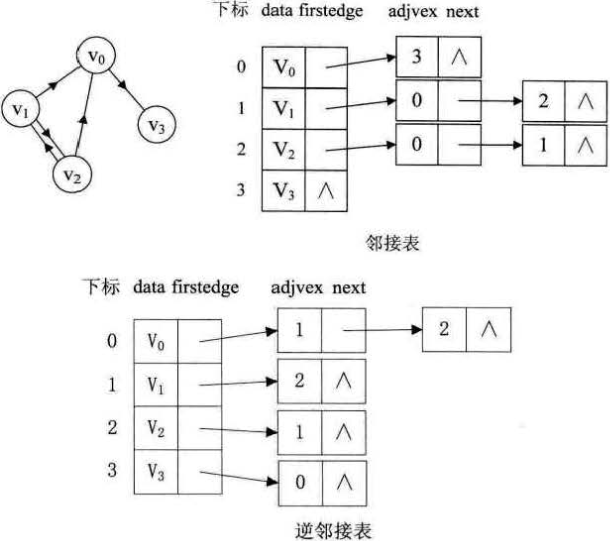
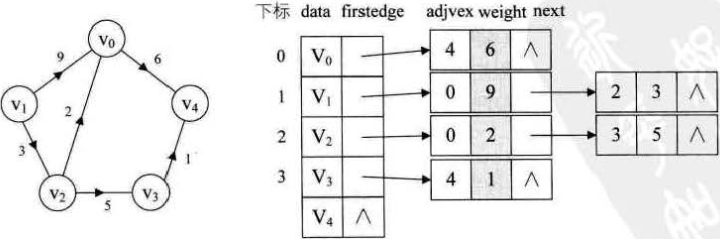
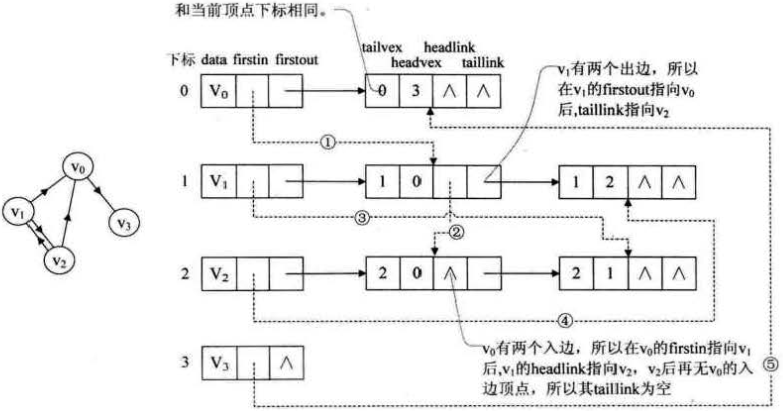
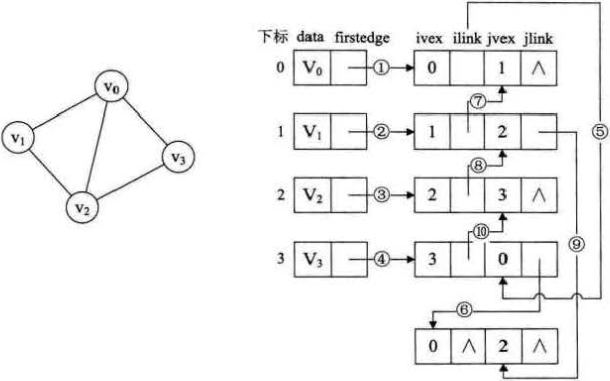
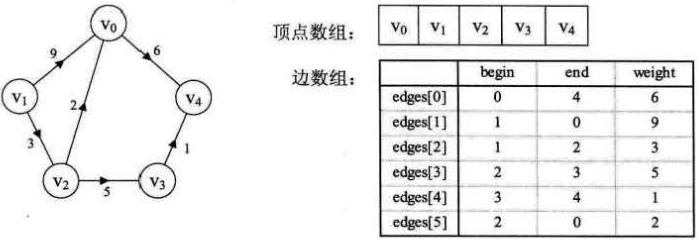
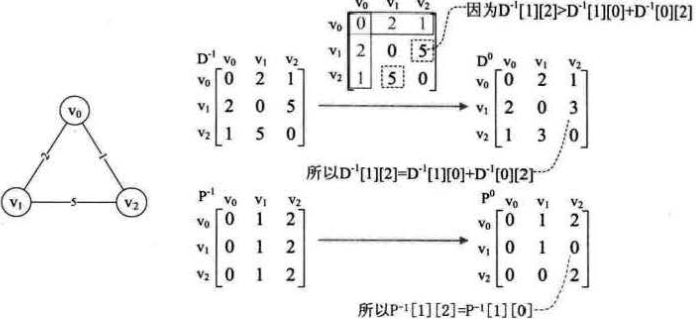
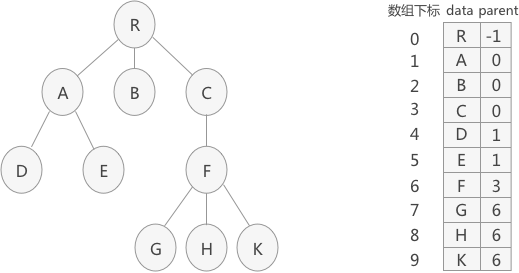
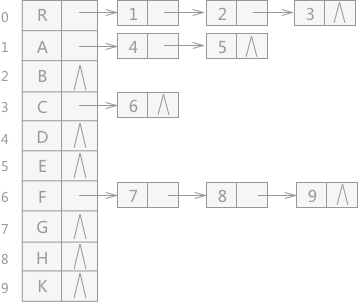
一、概念

bookkeeper 类似于一个日志存储系统。

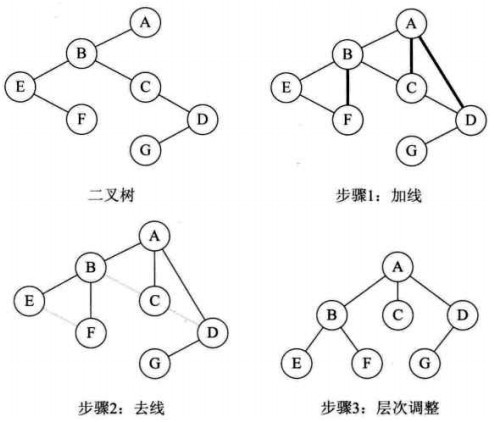
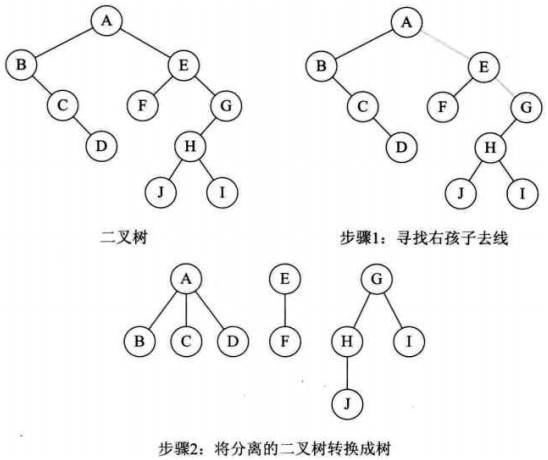
1. Ledger

Ledger 创建了之后，进行写数据、关闭和删除操作。

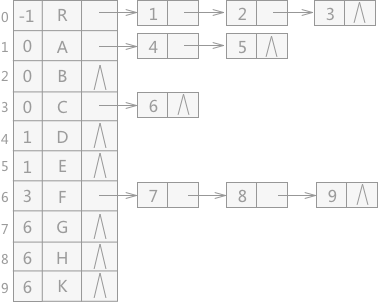
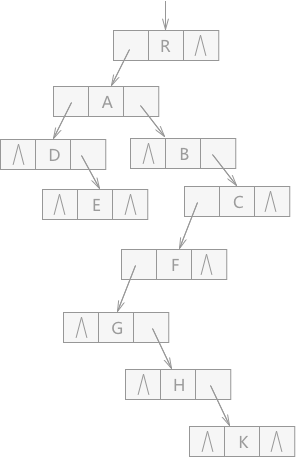
Legder 元数据的存储。结构如上图

参数的含义

state ：Ledger 的开关状态，open、close

last entry id : 上一次确认的entry id， entry id 是从 0 开始递增的

ensemble / write quorum / ack quorum ：ledger 存放位置的复制信息

2. Entry

entry 的元数据信息

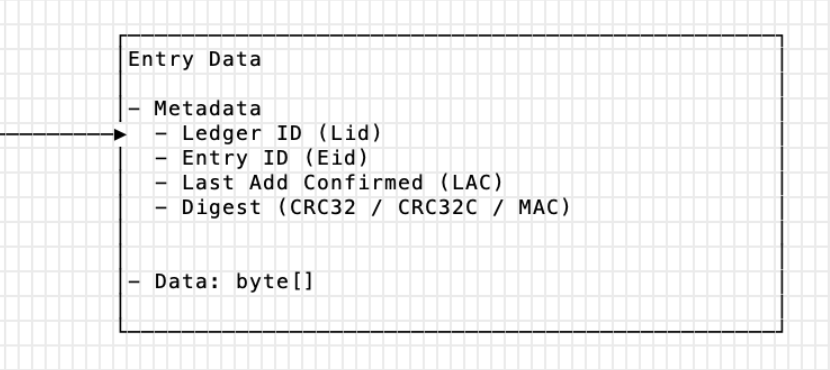
参数的含义

Lid 和 Eid ： 记录的是 entry 的key

LAC : 最后一条已经添加的记录

Digest ：记录字节的数据，用于完整性校验

上面介绍的 entry 和 Ledger 的元数据都会存入 Zookeeper 中。

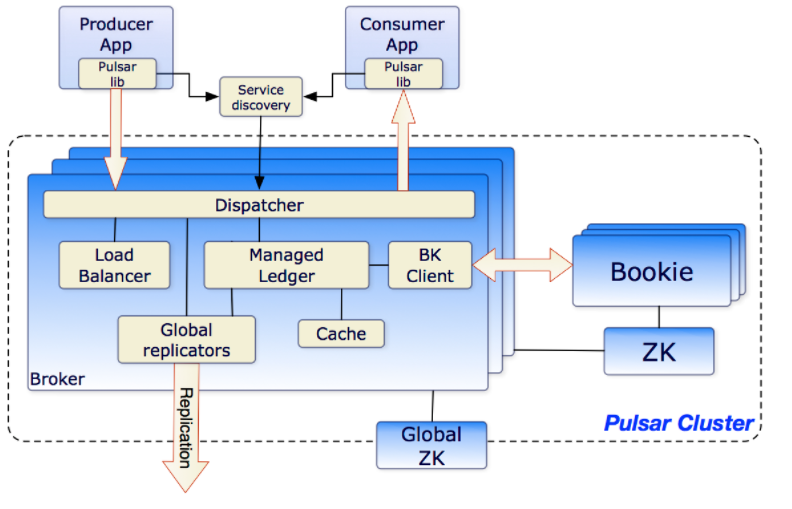
二、架构

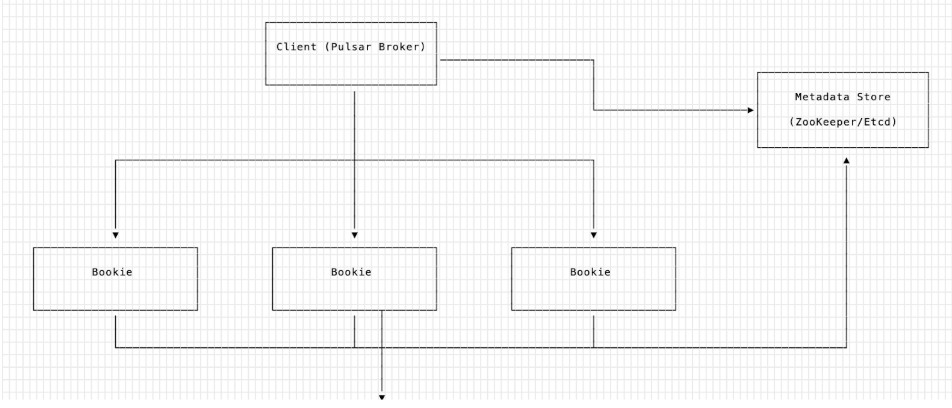
3大组件

1. zookeeper

存储元数据信息

2. client

实现一致性、策略性相关的逻辑

3. bookie

存储 ledger 对应的 entry ，所有的 bookie 都会存储到 Bookkeeper 上，让客户端发现

bookie 可以看做是一个 key-value 数据库。其中 key 就是 （lid + eid），value 就是 ledger 中的 entry 。

bookie 的实现是依靠 journal 和 ledger storage。

3.1 journal

journal 只有写操作，bookie 负责顺序把 entry 写到 journal 文件里，不会进行随机访问。

写满了一个 journal 之后，bookie 就会开启一个新的 journal 文件，继续按照顺序写 entry。

索引 write cache

journal 中的 entry 是没办法查询的，这个时候就需要索引来达到高效查询了。

write cache：bookie 端每次在写 entry 进 journal 的时候，会进行一个写缓存的操作。

写缓存的操作时，bookie 会对 entry 进行排序， 按 ledger 的来源进行划分，为了 entry 可以按照 ledger 进行排序。

当缓存写满时，bookie 会把 write cache 刷到磁盘中。flush 的过程中会进行重新整理成几个目录。一个是 ledger index，用来存储 entry key，一个是 entry log，用来存储 value。

3.2 ledger storage

两种方式，DB ledger storage 和 Sorted ledger storage，实现途径是一样的，就是索引存储的时候不太一样。

三、数据流动

bookie 的操作基本都是再客户端完成和实现的，比如副本复制、读写 entry 等操作。

data flow 是如何在客户端中实现的。

ledger 元数据中的几个参数

• Ensemble —— 用哪几台 bookie 去存储 ledger 对应的 entry
• Write Quorum ——对于一条 entry，需要存多少副本
• Ack Quorum —— 在写 entry 时，要等几个 response

默认情况下是（3,3,3），一共三个 bookie 去存储 ledger 对应的 entry，对于一个 entry，需要 3 个副本， 只有当3个 bookie 返回 response，才会确认。

四、恢复

1. Ledger Recovery

假设有一个 broker1 去写数据，不断地 append entry 到 ledger x ，当 T0 时间点更新 LAC 为 2， 这时发出的 entry3 是还没有得到请求回复的。这时的 entry3 的状态时 outstanding

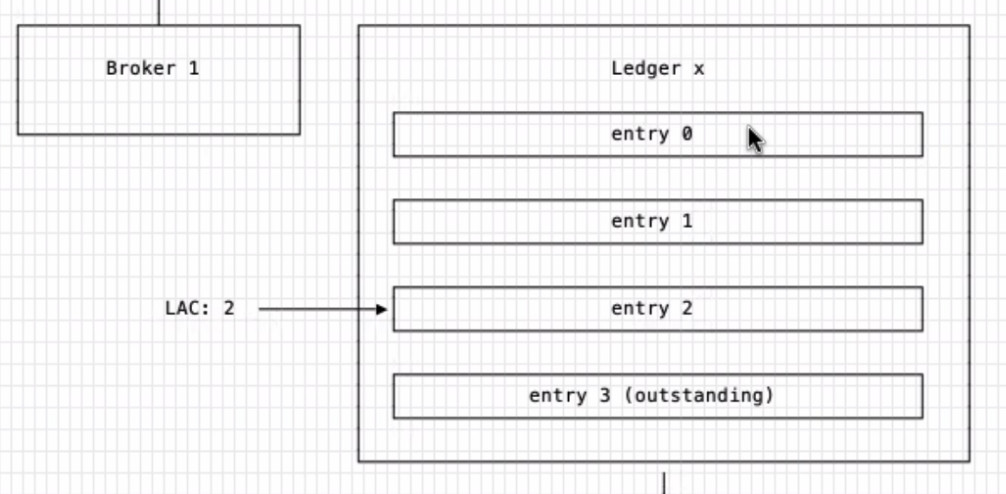
此时因为脑裂，broker2 去接管这个 topic 的写入， 尝试打开 ledger x 却发现他是 open 状态。 这个状态是无法继续进行读写操作的，那么 broker2 就对 ledger x 进行恢复操作 – Ledger Recovery

Ledger Recovery 流程

1. 此时返回当前 ledger 里最大的 LAC 数值，然后进行 recovery 的操作执行
2. 开始 recovery 操作之后，如果 broker1 还打算继续操作 ledger ，会收到 【操作失败】提醒，此时 broker1 知道当前这个 ledger 被其他 broker 使用后，会放弃所属权。
3. 由于 entry3 处于 outstanding 的状态， 还没有被写到 bookie 上。 继续往下读，发现没有 bookie 对下面的数据读写，就会采取关闭的操作，并将最后一条 entry 写回去。
4. 开启一个新的 ledger ，开始写入

2. Bookie Recovery

todo。。。。。

一、缓存概念

1. broker层面缓存

在 broker 层面里，存在一个 managed ledger 库，也就相当于 topic。也就是说每一个 topic 后边都有一个 managed ledger 进行服务存储等。

它会把 topic 里用到的所有 ledger 进行管理，并记录到元数据里。同时在消费订阅层面，也会将其订阅进度、消息签收进度等进行记录。

managed ledger cache ：新写入的数据会进行缓存

2. bookkeeper层面缓存

entry 写入 journal log 时，同时也会写入到 memory table 里，这时客户端认定为写入成功。这时会提出一个 check point，当满足 checkpoint 后，会把一段时间内的 journal log 数据放置到 entry log 里。而 index DB 则主要是记录 entry 放置在 entry log 的位置信息。

二、写入时优化

1. 开启分片

2. 加大内存

producer 生产消息时，是先把消息放到队列中的，如果队列满了，消息是会被阻塞的。

3. 批量消息

开启 batched 后，调动的 broker 数量减少，调用 bookie 次数也减少了，从而可以减少客户端和服务端的cpu使用，提升消息发送和读取的吞吐量。

4. 数据压缩

5. bookie 写入优化

消息持久化配置的选项，5-3-2 模式，会比 5-5-5的模式有更高的性能

6. 优化参数参考

Broker 端

1. managedLedgerDefaultEnsembleSize

2. managedLedgerDefaultWriteQuorum

3. managedLedgerDefaultAckQuorum

4. managedLedgerNumWorkerThreads

5. numIOThreads

6. Dorg.apache.bookkeeper.conf.readsystemproperties=true -DnumIOThreads=8

Bookie 端

1. Journal Directories

2. Ledger Directories

3. Journal sync data

4. Journal group commit

5. Write cache

6. Flush interval

7. Add worker threads and max pending add requests

8. Journal pagecache flush interval

三、读取时优化

1. 加大内存

消息读取其实跟写入差不多，也有一个 queue

2. 批量读取数据

3. 多consumer

4. 优化参数参考

Bookie 端

1. dbStorage_rocksDB_blockCacheSize

2. dbStorage_readAheadCacheMaxSizeMb

3. dbStorage_readAheadCacheBatchSize

4. Read worker threads

Broker 端

1. Managed ledger cache

2. Dispatcher max read batch size

3. Bookkeeper sticky reads

一、Topic Discovery

1. Topic Assignment

首先看一下层次化结构

根据图上所示，topic 的分配是按照 namespace 来划分的

一个 namespace 下面会有很多个 topic，namespace 会把所有的 topic 组成一个环（namespace hash ring）。在 topic 分配之前，会把 topic 的名字 hash 到 namespace hash ring 里。然后根据不同 topic 的 hash 值 又会分为几个小组， 也就是 namespace bundle， bundle 的数量可以在创建 namespace 时就可以指定确认了。

topic 映射 到 bundle 后，接下来就会将 bundle 分配给 broker。 也就是 topic 的分配不在于 topic 本身，而是 bundle 操作。处理过程依靠 load Maneger 进行，对 bundle 进行分配。

load manager 是从 broker 中选出来的一台。 topic 分配到 broker 的过程，全程是由 load manager 来执行的。

2. Topic lookup

topic 如何找到对应的那台 broker呢？

先介绍一个概念：Topic owner ，又可以称为 namespace bundle owner 。

topic 与 broker 的映射关系，存储在 owner 中， owner存储在zookeeper中，任何一个 broker 都可以获取到 topic 到 owner 的映射关系。

lookup 流程：

pulsar 客户端发起 topic lookup 请求给 broker，broker 开启 lookup模式，根据 namespace 去检测出映射的 bundle， 然后将此反馈发给 zookeeper 去查找对应，最后将请求结果返回给客户端。

客户端这时， 会根据请求结果和目标 broker 进行 tcp 长链接。

有个问题，这个时候如果目标 broker 的地址不能直接链接，该怎么办？

解决方案：

使用 pulsar proxy 。它提供了 topic 查询路由功能，可以作为 tcp 反向代理来使用

二、ServiceURL

知道了整个 topic discovery 之后。对 service URL 的使用就会更加准确了

service URL 高可用的几种方式

DNS：在 broker 之前配置一个 DNS，落实到 broker 里。 缺点是 过期时间和缓存限制

Load Balance：可以探测活跃的 broker，可以及时清理 broker。

Multi-Hosts：把所有机器当做一个列表，pulsar客户端进行负载均衡，第一次用第一个broker，链接失败用第二个，以此类推

三、Clusters

部署 pulsar 集群的时候，需要制定 cluster name， 集群配置信息作为元数据保存到 zookeeper 上。

在 cluster 配置文件里，主要是四个接入端口，分为两大类。

HTTP service：即提供 admin 操作的接口

• Web service URL (http://)
• Web service URL TLS (https://)

Broker service：即客户端、producer、consumer 等需要连接的 6650 端口。

• Broker service URL (pulsar://)
• Broker service URL TLS (pulsar+ssl://)

这几个参数只有在进行跨机房复制时才使用。

在介绍消息的生命周期之前，先看一下 pulsar 的架构

一、pulsar 集群

1. Brokers + Bookies

broker 是各个组件之间进行交互的对象。pulsar 是分层架构模式，使用 Bookkeeper 作为额外的存储系统， bookies 就是 Bookkeeper 里的存储节点。

Brokers + Bookies 构成 pulsar 的两个层次， 共同完成 pulsar 的数据服务

Broker： 整个消息层的生产和消费，无存储状态

Bookie： 数据持久化保存的节点，有存储状态

2. Zookeeper

Zookeeper 在 Pulsar 里的作用是存储 Pulsar 系统里的元数据和集群的管理以及节点的发现等，节点发现就是发现集群中有哪些 broker 哪些 bookie 。

以上的三个组件，构成了 Pulsar 的集群。Brokers + bookies 为数据服务，Zookeeper 为元数据服务。

二、message lifecycle

1. producer 生产消息（写过程）

producer 通过生产消息到一个 topic， 一个 topic 中可能有 N 个 partition， 每个 partition 给一个 broker 服务。

生产者内部有一个 MessageWriter 的类， 这个 MessageWriter 默认是 round-robin 的过程，就是发送每条消息的时候回去轮训找到一个 partition 进行发送，但为了提高效率，在一段时间内只会选择一个 partition 进行发送。如果 message 指定了 key，那么会根据 key 的hash去找到对应的 partition 进行发送。

之后 Broker 收到消息后会调用 BookKeeper 的客户端并发去写多个 bookie 副本。当 broker 收到一定数量的 ACK 后，他会认为消息已经写入成功，broker 返回客户端，告知这条消息已经被持久化完成。

整个写的过程消息是从 producer 到 broker，broker 到 Bookkeeper 上。 整个过程中客户端都不会跟Zookeeper打交道，也不会和 Bookkeeper打交道， 只和 Broker 打交道。

2. consumer 消费消息（读过程）

2.1 broker 有缓存的情况下

Broker 可能已经缓存了部分信息，consumer 在连接到 broker 后建立长链接， broker 把消息从内存里拿出来通过推得方式 dispatch 给 consumer， consumer 收到消息后会放到消费端的 receiver queue 中，consumer 就可以消费了，完了发送确认ack给broker。

2.2 broker 没有缓存的情况下

broker 没有缓存这部分数据，需要去 bookie 去读取数据， 数据读取出来后再 dispatch 给 consumer，读取是选择任意一个存储节点读取的，整个存储架构没有主节点的说法。

3. Data Retention

3.1 Subscription Initial Position

之前整理了 subscription 和 cursor 的概念。如果有个新的订阅是pulsar中没有的，那么如何创建 cursor？

这里就有两个概念

earliest：放到整个流中第一条有效数据

latest: 放到整个流中最后一条有效数据 (默认的)

Cursor 放置的位置，决定了最终消费了什么数据

3.2 Message Retention

消费位置最早的订阅决定了你能保留消息多久，订阅之前的消息可以被删除。这是 pulsar 的默认行为， 即消费完就可以被删除， 释放空间留给之后的消息使用。

由于流计算的需求，有些数据消费完还不能删除，需要再额外保留个三五天。就需要 retention 来进行数据的保留设置

添加后 retention 后, 紫色部分的内容就是该保留的数据，可以配置多大内存/多少天。但前提是被所有订阅消费完了

3.3 TTL

还有一种情况就是，生产者一直在生产消息，但是消费者一直没有处理，那么消息永远不会被确认，那么这个消息会被一直累积。

为了保障消息不会被一只累加下去，可以在这写橘色消息部分加上TTL，TTL作用范围是没被确认的消息。

在TTL之后，消息会到Retention中，然后再经理过Retention中设置的时间，进行最后的数据清除。

3.4 Message Deletion

正常理解是，消息过期后就会被删除，但是在pulsar中，消息的删除是按照 片（segment） 进行的。

例如上图，删除的是 S1 这个分片，而S2 不会被删除，因为只有分片中所有的消息是待删除状态，才会去删除这个分片。

3.5 storage size

storage size是计算所有没被删除的 segment 所占用的存储空间。

整个存储空间是按照 segment 之间的存储力度进行计算的，同时 garbage collector 是定时执行的，所有有时候可以发现 segement 已经被清空了，但是 storage size 仍然没有变化。

一、前言

Pulsar 是一个用于服务器到服务器的消息系统，具备高吞吐，低延迟，计算存储分离，多租户，异地复制等特性，这些特性也使得Pulsar成为kafka的有力竞争者

二、Pub/Sub

下面介绍pulsar做为一个发布订阅消息中间件的一些主要概念

• Message
• Producer
• Consumer
• Broker
• Topic
• Subscription

1. Message

消息是 Pulsar 的基础单元，Producer 发送消息，Consumer 消费消息，Broker 保存消息。

1.1 消息的组成

1. data：数据
2. key：消息键，非常重要的一个概念，消息的发送和路由都与它有关
3. property：键值对，存放一些主数据之外的额外消息
4. producer name：消费者名
5. sequence id: 序列号。消息去重会使用到这个参数，相同的序列号只会发送一次
6. publish time：发布时间
7. event time: 事件事件
8. TypedMessageBuilder: 用于构建消息

2. Producer

Producer 可以发送消息到指定的 topic。往 Pulsar 里发送消息时，相应的数据会带上 schema 的信息。Pulsar 会确保一个 producer 往 topic 发送的消息是满足一定的 schema 格式。

2.1 发送模式

同步发送send，异步发送sendAsync

2.2 批量处理

通过设置enableBatching、batchingMaxMessages、maxPendingMessages等，来设置批量消息的发送规则。

2.3 消息压缩

通过设置compressionType，来指定压缩类型

2.4 分块

分块的前提是禁用批量处理

3. Consumer

consumer与broker建立TCP长链接，然后开始接受从broker的推送来的消息。同时也会根据schema来格式化消息

3.1 接收模式

同步接收

异步接收，返回一个CompletableFuture

3.2 ACK

确认消息/取消确认：消费者成功/失败消费一条消息，这条消费者会发送一个确认消息/取消确认给broker。成功的话，这条消息会根据消息保留策略来进行删除。

3.3 监听器

通过MesssageListener可以监听接受的每条消息，通过received方法进行逻辑处理

3.4 死信、重试队列

设置了死信队列，消费者消费一条消息时，当超时或者否定确认，这条消息会被重新传递，当多次的重新传递后，这条消息会被放入到指定的死信topic中。

重试队列，当消费者消费一条消息时，当超时或者否定确认，默认会进行重试。

3.5 Cursor 和 Reader

Cursor 在消费者端，代表了每组订阅组的消费状态。 broker 的 cursor 会追踪每个订阅消费到了哪里，然后记录下来。

Reader 和 Cursor 不同， cursor 是 pulsar帮你管理消费状态信息，但是 Reader 是一个没有状态的，消息被消费了，它消费状态不会持久化。也就是下次再读取的时候还是能读取到。

4. Broker

分区落靠的服务器，就是 Broker。Broker 用来接收与发送消息，生产方连接到 broker 去生产消息，消费方连接到 broker 去消费消息。

数据不会存储在 Broker 上，是放在 Bookkeeper 中。这也是 Pulsar 与其他中间件的区别。

5. Topic

topic是消息的集合，所有的producer的消息，都会归属到指定的topic里。所有topic里的消息，会按照一定的规则，被切分成不同的分区（Partition）。一个分区会落到一台broker上。

topic格式：{persistent|non-persistent}://tenant/namespace/topic

pulsar层级化的管理，使用 Tenant 和 namespace。

6. Subscription

consumer 连接到 broker，需要定义自己的 Subscription ，一个订阅的所有 consumer 会作为一个整体去消费 topic 里的所有消息。

6.1 订阅模式

四种模式：Exclusive、Failover、Shared、Key_Shared

Exclusive：只有一个 consumer 可以消费消息。

Failover：一个消费者作为一个主题分区( partition, 一个 topic 会有多个 partition ) 的主使用者，其他消费者被作为故障转移备用。

Shared: 消息会轮训发送给该订阅下的所有 consumer 。

Key_Shared：消息按照 key 进行分发给 consumer。融合了 Failover 和 Shared 的特性。

三、schema

Schema 的作用就是如何序列化反序列化数据，不用在客户端另外去做处理。

schema 的格式

• type：schema类型
• schema：schema 定义，和数据
• properties：跟 schema 关联的部分属性

两类 schema

• key-value：要同时定义 key schema 和 value schema，将这两者的信息组合在一起放置在 schema 信息文件内
• struct ：AVRO、JSON、Protobuf 三种类型

schema 的兼容性检查

概念

**堆(Heap)**是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。

1、二叉堆

二叉堆是完全二元树或者是近似完全二元树，按照数据的排列方式可以分为两种：最大堆和最小堆。

二叉堆一般都通过”数组”来实现

2、左倾堆

左倾堆(leftist tree 或 leftist heap)，又被成为左偏树、左偏堆，最左堆等。

它和二叉堆一样，都是优先队列实现方式。可以高效解决”对两个优先队列进行合并”的问题。

上图是一颗左倾树，它的节点除了和二叉树的节点一样具有左右子树指针外，还有两个属性：键值和零距离。

• 键值：作用是来比较节点的大小，从而对节点进行排序。
• 零距离：是从一个节点到一个”最近的不满节点”的路径长度。不满节点是指该该节点的左右孩子至少有有一个为NULL。叶节点的NPL为0，NULL节点的NPL为-1。

左倾堆有以下几个基本性质：

• 节点的键值小于或等于它的左右子节点的键值。
• 节点的左孩子的NPL >= 右孩子的NPL。
• 节点的NPL = 它的右孩子的NPL + 1。

合并两个左倾堆的基本思想如下：

1. 如果一个空左倾堆与一个非空左倾堆合并，返回非空左倾堆。
2. 如果两个左倾堆都非空，那么比较两个根节点，取较小堆的根节点为新的根节点。将”较小堆的根节点的右孩子”和”较大堆”进行合并。
3. 如果新堆的右孩子的NPL > 左孩子的NPL，则交换左右孩子。
4. 设置新堆的根节点的NPL = 右子堆NPL + 1

3、斜堆

斜堆也叫自适应堆，它是左倾堆的一个变种。和左倾堆一样，它通常也用于实现优先队列；作为一种自适应的左倾堆，它的合并操作的时间复杂度也是O(log n)。

它与左倾堆的差别是：

1. 斜堆的节点没有”零距离”这个属性，而左倾堆则有。
2. 斜堆的合并操作和左倾堆的合并操作算法不同。

斜堆的合并操作

1. 如果一个空斜堆与一个非空斜堆合并，返回非空斜堆。
2. 如果两个斜堆都非空，那么比较两个根节点，取较小堆的根节点为新的根节点。将”较小堆的根节点的右孩子”和”较大堆”进行合并。
3. 合并后，交换新堆根节点的左孩子和右孩子。

第 3 步是斜堆和左倾堆的合并操作差别的关键所在，如果是左倾堆，则合并后要比较左右孩子的零距离大小，若右孩子的零距离 > 左孩子的零距离，则交换左右孩子；最后，在设置根的零距离。

4、二项堆

二项堆是二项树的集合。在了解二项堆之前，先对二项树进行介绍。

1）二项树

二项树是一种递归定义的有序树。它的递归定义如下：

1. 二项树B0只有一个结点；
2. 二项树Bk由两棵二项树B(k-1)组成的，其中一棵树是另一棵树根的最左孩子。

2）二项堆

二项堆和之前所讲的堆(二叉堆、左倾堆、斜堆)一样，也是用于实现优先队列的。二项堆是指满足以下性质的二项树的集合：

1. 每棵二项树都满足最小堆性质。即，父节点的关键字 <= 它的孩子的关键字。
2. 不能有两棵或以上的二项树具有相同的度数(包括度数为0)。换句话说，具有度数k的二项树有0个或1个。

5、斐波那契堆

斐波那契堆(Fibonacci heap)是一种可合并堆，可用于实现合并优先队列。它比二项堆具有更好的平摊分析性能，它的合并操作的时间复杂度是O(1)。

与二项堆一样，它也是由一组堆最小有序树组成，并且是一种可合并堆。

与二项堆不同的是，斐波那契堆中的树不一定是二项树；而且二项堆中的树是有序排列的，但是斐波那契堆中的树都是有根而无序的。

6、索引堆

索引堆是对堆进行了优化。

索引堆使用了一个新的int类型的数组，用于存放索引信息。

索引堆的交换操作交换的是元素的索引，而不是直接交换元素。

7、Treap 树堆

一棵treap是一棵修改了结点顺序的二叉查找树，如图，显示一个例子，通常树内的每个结点x都有一个关键字值key[x]，另外，还要为结点分配priority[x]，它是一个独立选取的随机数。

假设所有的优先级是不同的，所有的关键字也是不同的。treap的结点排列成让关键字遵循二叉查找树性质，并且优先级遵循最小堆顺序性质：

1. 如果v是u的左孩子，则key[v] < key[u].
2. 如果v是u的右孩子，则key[v] > key[u].
3. 如果v是u的孩子，则priority[u] > priority[u].

这两个性质的结合就是为什么这种树被称为“treap”的原因，因为它同时具有二叉查找树和堆的特征。

一、图的基本概念

图：由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为: G(V,E)，其中，G 表示一个图，V 是图 G 中顶点的集合。E 是图 G 中边的集合。

1、各种图定义

• 无向边：若顶点 V_i 到 V_j，之间的边没有方向，则称这条边为无向边(Edge)。
  • 用无序偶对 (V_i，V_j) 来表示。
• 有向边：若从顶点 V_i 到 V_j的边有方向，则称这条边为有向边，也称为弧（Arc）。
  • 用有序偶<V_i，V_j>来表示 . V_i称为弧尾，V_j称为弧头。
• 无向图：如果图中任意两个顶点之间的边都是无向边，则称该图为无向图(Undirected graphs)。
• 有向图：如果图中任意两个顶点之间的边都是有向边，则称该图为有向图(Directed graphs)。
• 无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该因为无向完全图。
  • 含有 n 个顶点的无向完全图有 n(n-1)/2 条边。
• 有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。
  • 含有 n 个顶点的有向完全图有 n*(n-1) 条边
• 权：与图的边或弧相关的数叫做权(Weight)
• 网：带权的图通常称为网 (Network) 。
• 简单图：在图中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。
• 有很少条边或弧的图称为稀疏图，反之称为稠密图。稀疏、稠密是相对的。
• 子图：假设有两个图 G= (V,{E}) 和 G’= (V’,{E’}) ，如果 V'为 V的子图 且 E'为 E的子图，则称 G’ 为 G 的子图。

2、图的顶点与边间关系

• 邻接点：无向图中，顶点之间如有边相连，则互为邻接点
• 顶点的度：记为TD(v)
  • 无向图中，和顶点相关联的边的数目，就是顶点的度
  • 有向图中，TD(v) = ID(v) + OD(v)
    • 入度：有向图中，以顶点为头的弧的数目，记为ID(v)
    • 出度：有向图中，以顶点为尾的弧的数目，记为OD(v)
• 路径：
  • 无向图中，顶点到顶点的路径是一个顶点序列
  • 有向图中，路径也是有向的
  • 路径的长度：是路径上的边或弧的数目。
• 回路或环：第一个顶点到最后一个顶点相同的路径称为回路或环
• 简单路径：序列中顶点不重复出现的路径称为简单路径
• 简单回路：除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。

3、连通图相关术语

• 连通：无向图中，如果顶点间有路径，则称为连通的
• 连通图：无向图中，如果图中任意两个顶点都是连通的，则为连通图
• 强连通图：有向图中，每一对顶点之间都相互存在路径，则为强连通图
• 连通分量：无向图中的极大连通子图称为连通分量
• 强连通分量：有向图中的极大强连通子图称做有向图的强连通分量。
• 生成树：无向图中连通且有 n 个顶点 n-l 条边。
• 有向树：有向图恰有一个顶点的入度为 0 ，其余顶点的入度均为 1。
• 生成森林：一个有向图的生成森林由若干棵有向树组成 ， 含有图中全部顶点，但只有足以构成若干棵不相交的有向树的弧。

二、图的存储及基本操作

1、邻接矩阵：适合稠密图

邻接矩阵 (Adjacency Matrix)用两个数组来表示图：

• 一维数组：存储图中顶点信息

• 二维数组：存储图中的边或弧的信息。

1）无向图

• 无向图的边数组是一个对称矩阵
• 有无边：arc[i][j] 是否为 1
• 顶点的度：顶点v_i在邻接矩阵中第 i 行(或第 i列)的元素之和
• 邻接点：邻接矩阵中第 i 行元素值为 1 就是顶点v_i的邻接点。

2）有向图

• 有向图的矩阵不对称。
• 有无弧：arc[i][j] 是否为 1
• 入度：第 i 行元素之和
• 出度：第 i 列元素之和
• 邻接点：第 i 行元素值为 1 的

3）网

网的对应边或弧存权值

2、邻接表：适合稀疏图

邻接表(Adjacency List) 使用数组与链表相结合存储图

• 一维数组：存顶点，和指向第一个邻接点的指针
• 单链表：存每个顶点的所有邻接点。邻接点在顶点表中的下标，

1）无向图

• 度：顶点的边表中结点的个数
• 是否存在边：测试定点边表中是否存在结点下标
• 邻接点：顶点的边表

2）有向图

以顶点为弧尾来存储边表

有向图的逆邻接表：以顶点为弧头的边表

3）网

在边表结点定义中再增加一个 weight 的数据域，存储权值信息

3、十字链表：适合有向图

对于有向图来说，邻接表是有缺陷的。出度入度只能关心一个。

十字链表把邻接表与逆邻接表结合起来。

• 一维数组：顶点表结点
  • data
  • firstin：入边表头指针
  • firstout：出边表头指针
• 边表结点：
  • tailvex：弧起点在顶点表的下标
  • headvex：弧终点在顶点表中的下标
  • headlink：入边表指针域
  • taillink ：边表指针域
  • weight：如果是网，存储权值

实线箭头指针的图示与邻接表相同。虚线箭头是逆邻接表的表示。

4、邻接多重表：适合处理无向图的边

ivex 和 jvex 是与某条边依附的两个顶点在顶点表中下标。ilink 指向依附顶点 ivex 的下一条边， jlink 指向依附顶点 jvex 的下一条边。这就是邻接多重表结构。

邻接多重表与邻接表的差别，仅仅是在于同一条边在邻接表中用两个结点表示，而在邻接多重表中只有一个结点。

5、边集数组：适合对边依次处理

边集数组是由两个一维数组构成。一个是存储顶点的信息;另一个是存储边的信息，这个边数组每个数据元素由一条边的起点下标 (begin) 、终点下标 (end) 和权(weigbt) 组成

三、图的遍历

图的遍历(Traversing Grapb)：从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次

1、深度优先搜索

深度优先遍历(Depth_First_Search)，也有称为深度优先搜索，简称为 DFS。

类似于树的前序遍历，用数组记录访问：

1. 访问初始结点v，并标记结点v为已访问。
2. 查找结点v的第一个邻接结点w。
3. 若w存在，则继续执行4，否则算法结束。
4. 若w未被访问，对w进行深度优先遍历递归（即把w当做另一个v，然后进行步骤123）。
5. 查找结点v的w邻接结点的下一个邻接结点，转到步骤3。

2、广度优先搜索

广度优先遍历 (Breadth.First.Search) ，又称为广度优先搜索，简称 BFS。

类似于树的分层遍历，用队列保持访问过的结点的顺序：

1. 访问初始结点v并标记结点v为已访问。
2. 结点v入队列
3. 当队列非空时，继续执行，否则算法结束。
4. 出队列，取得队头结点u。
5. 查找结点u的第一个邻接结点w。
6. 若结点u的邻接结点w不存在，则转到步骤3；否则循环执行以下三个步骤：
   1. 若结点w尚未被访问，则访问结点w并标记为已访问。
   2. 结点w入队列
   3. 查找结点u的继w邻接结点后的下一个邻接结点w，转到步骤6。

四、图的基本应用

1、最小（代价）生成树

最小生成树： 一个具有n个顶点的加权的无向连通图，用n-1条边连接这n个顶点，并且使得连接之后的所有边的权值之和最小的树。

1）普里姆 ( Prim )算法

1. 将点分为两拨，已经加入最小生成树的，未加入的
2. 找到未加入中距离集合最近的点，添加该点，修改其它点到集合的距离
3. 直到所有结点都加入到最小生成树

2）克鲁斯卡尔( Kruskal )算法

1. 现将所有边进行权值的从小到大排序
2. 定义一个一维数组代表连接过的边，数组的下标为边的起点，值为边的终点
3. 按照排好序的集合用边对顶点进行依次连接，连接的边则存放到一维数组中
4. 用一维数组判断是否对已经连接的边能构成回路，有回路则无效，没回路则是一条有效边
5. 重复3，4直至遍历完所有的边为止，即找到最小生成树

2、最短路径

对于网图来说，最短路径，是指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点。

1）迪杰斯特拉( Dijkstra ) 算法

适用于求一个节点到其他节点的最短路径，通过广度搜索来遍历其他所有需要求距离的点。

1. 选取初始节点作为一个集合，D(v)表示初始节点到V节点的最短路径
2. 所有能直接到达V的节点路径记为 D(v)=距离，不能直接到达的节点路径记为 D(v)=无穷
3. 选取 D(v) 最小的节点加入初始节点集合，最短路径记为D(w)=min(D(w),D(v)+j(v,w))（j(v,w)为节点V到W的距离）
4. 重复步骤3，直到所有节点都加入初始节点集合

2）弗洛伊德( Floyd )算法

适用于求所有顶点至所有顶点的最短路径问题。

1. 确定一个中间点
2. 定义两个二维数组 D[][] 和 P[][]
   • D 代表顶点到顶点的最短路径权值和的矩阵，即点的邻接矩阵
   • P 代表对应顶点的最小路径的前驱矩阵
3. 对于每一对顶点 v 和 w，看看是否存在一个顶点 u 使得从 v 到 u 再到 w 比己知的路径更短。

3、拓扑排序

• AOV：有向无环图
• 拓扑序列：是一个有向无环图的所有顶点的线性序列。
  • 每个顶点出现且只出现一次。
  • 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。
• 拓扑排序：对一个有向图构造拓扑序列的过程
  • 从 AOV 中选择一个入度为0的顶点并输出。
  • 从图中删除该顶点，井删除以此顶点为尾的弧
  • 重复此步骤，直到输出全部顶点，或不存在入度为0的顶点为止。

建立一个邻接表，在顶点表结点结构中，增加一个人度域 in

4、关键路径

• AOE：有向无环网
• 路径长度：路径上各个活动所持续的时间之和
• 关键路径：从源点到汇点具有最大长度的路径
• 关键活动：在关键路径上的活动

关键路径算法

1. 事件最早开始时间（etv）：顶点v_k最早发生的时间。
2. 事件最晚开始时间（ltv）：顶点v_k最晚发生的时间，超出则会延误整个工期。
3. 活动的最早开始时间（ete）：弧a_k最早发生时间。
4. 活动的最晚开始时间（lte）：弧a_k最晚发生时间。不推迟工期的最晚开工时间。

由 1 和 2 可以求得 3 和 4 ，然后再根据 ete[k] 是否与 lte[k] 相等来判断a_k是 否是关键活动。

建立一个邻接表，弧链表增加了 weight 域，用来存储弧的权值。

• 先要调用一次拓扑序列算法的代码来计算etv和拓扑序列表。
• 数组etv存储事件最早发生时间
• 数组ltv存储事件最迟发生时间
• 全局栈用来保存拓扑序列

如果是多条关键路径，则单是提高一条关键路径上的关键活动速度并不是能导致整个工程缩短工期、而必须提高同时在几条关键路径上的活动的速度。

一、树的基本概念

树：是 n ( n>=0 ) 个结点的有限集。

• n = 0 时称为空树。
• 在任意一棵非空树中:
  • 有且仅有一个根结点
  • 当 n > 1 时，其余结点可分为一个或多个互不相交的有限集。 其中每一个集合本身又是一棵树，并且称为根的子树。

1、结点分类

• 结点的度：结点拥有的子树数
• 叶结点：度为 0 的结点
• 分支结点：度不为 0 的结点
• 树的度：树内各结点的度的最大值

2、结点间关系

• 孩子：结点的子树的根称
• 双亲：上一结点
• 兄弟：同一个双亲的孩子
• 祖先：从根到该结点所经分支上的所有结点

3、树的其他相关概念

• 层次：根开始定义起，根为第一层 ，根的孩子为第二层
• 堂兄弟：双亲在同一层的结点
• 树的深度：树中结点的最大层次
• 有序树：树中结点的各子树从左至右有次序，不能互换
• 无序树：非有序树
• 森林：m (m>=0) 互不相交的树的集合

二、二叉树

1、二叉树的定义

二叉树：是 n(n >= 0) 个结点的有限集合，该集合或者为空集(称为空二叉树)，或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

1）主要特征

• 每个结点最多有两棵子树，所以二叉树中不存在度大于 2 的结点。
• 左子树和右子树是有顺序的，次序不能任意颠倒。
• 即使树中某结点只有一棵子树，也要区分它是左子树还是右子树.

2）特殊二叉树

• 斜树：都只有一边子结点
  • 左斜树：所有的结点都只有左子树的二叉树
  • 右斜树：所有结点都是只有右子树的二叉树
  • 线性表结构可以理解为是树的一种极其特殊的表现形式
• 满二叉树：每层结点都排满了
• 完全二叉树：按层排序，到结尾中间没有漏掉的结点

3）二叉树性质

• 在二叉树的第 i 层上至多有 2^{i-1} 个结点 (i >= 1 ) 。

• 深度为 k 的二叉树至多有2^k-1个结点 (k >= l) 。

• 对任何一棵二叉树 T，如果其终端结点数为 n_0，度为 2 的结点数为 n_2，则 n_0 = n_2 +1。

• 具有 n 个结点的完全二叉树的深度为 [log_2n]+1 ([x] 表示不大于 x 的最大整数)。

• 如果对一棵有 n 个结点的完全二叉树(其深度为 [log_2n]+1 ) 的结点按层序编号(从第 1 层到第 [log_2n]+1层，每层从左到右) ，对任一结点 i (1<= i<= n)有:

  • 如果 i = 1 ，则结点 i 是二叉树的根，无双亲；如果 i > 1 ，则其双亲是结点 [i/2]。

• 如果 2i > n ，则结点 i 无左孩子(结点 i 为叶子结点)；否则其左孩子是结点 2i。

  • 如果 2i+1 > n ，则结点 i 无右孩子；否则其右孩子是结点 2i+1 。

2、二叉树的存储结构

1）顺序存储结构

顺序存储结构一般只用于完全二叉树。

用一维数组存储二叉树中的结点，数组的下标和结点序号一致。没有结点的存空。

2）链式存储结构

二叉链表：一个数据域和两个指针域的链表。

指针域分别存左孩子和右孩子的指针。

3、二叉树的遍历

1）遍历方法

• 前序遍历：根节点->左子树->右子树
• 中序遍历：左子树->根节点->右子树
• 后序遍历：左子树->右子树->根节点
• 层序（宽度优先、广度优先）遍历：每一层从左向右输出

前序、中序、后序遍历用迭代很简单。

层序遍历，元素储存有先进先出的特性，选用队列。

2）遍历推导

• 己知前序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。
• 已知后序遍历序列和中序遍历序列，可以唯一确定一棵二叉树 。
• 已知前序和后序遍历，是不能确定一棵二叉树的

3）二叉树的建立

扩展二叉树：将每个结点的空指针引出一个虚结点，值为特定值（如“#”）

扩展二叉树可以用递归采用前序、中序、后序遍历的一个遍历序列就确定一颗二叉树。

4、线索二叉树

1）基本概念

• 线索：指向前驱和后继的指针称为线索
• 线索链表：加上线索的二叉链表称为线索链表
• 线索化：将二叉链表中的空指针改为指向前驱或后继的线索

线索二叉树，等于是把一棵二叉树转属变成了一个双向链表，对插入删除结点、查找某个结点都带来了方便

2）构造

每个结点增设两个标志域 ltag 和 rtag，区分指针是指向孩子还是指向前驱、后继。

在遍历的过程中修改空指针。

如果所用的二叉树需经常遍历或查找结点时需要某种遍历序列中的前驱和后继，那么采用线索二叉链表的存储结构就是非常不错的选择。

三、树、森林

1、树的存储结构

1 ）双亲表示法

除了根结点外，其余每个结点，它不一定有孩子，但是一定有且仅有一个双亲。以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指示其双亲结点到链表中的位置。

存储结构的设计是一个非常灵活的过程。

• 双亲域：增加一个结点指示其双亲结点的域
• 长子域：增加一个结点最左边孩子的域
• 右兄弟域：增加一个右兄弟域体现兄弟关系

当算法中需要在树结构中频繁地查找某结点的父结点时，使用双亲表示法最合适。当频繁地访问结点的孩子结点时，双亲表示法就很麻烦，采用孩子表示法就很简单。

2）孩子表示法

由于树中每个结点可能有多棵子树，可以考虑用多重链表，即每个结点有多个指针域，其中每个指针指向一棵子树的根结点，我们把这种方法叫做多重链表表示法。

• 方案一：指针域的个数就等于树的度
  • 树中各结点的度相差很大时，浪费空间
• 方案二：每个结点指针域的个数等于该结点的度
  • 各个结点的链表是不相同的结构，还要维护结点的度的数值，浪费运算时间

孩子表示法

把每个结点的孩子结点排列起来，以单链表作存储结构，则 n 个结点有 n 个孩子链表，如果是叶子结点则此单链表为空。然后 n 个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中

双亲孩子表示法

使用孩子表示法存储的树结构，正好和双亲表示法相反，适用于查找某结点的孩子结点，不适用于查找其父结点。可以将两种表示方法合二为一

孩子兄弟表示法

把一棵复杂的树变成一棵二叉树

链表中每个结点由 3 部分组成：

• 孩子指针域：表示指向当前结点的第一个孩子结点
• 数据域
• 兄弟指针域：表示指向当前结点的下一个兄弟结点

2、树、森林与二叉树的转换

1）树转换为二叉树

1. 加线。在所有兄弟结点之间加一条连线。
2. 去钱。对树中每个结点，只保留它与第一个孩子结点的连线，删除色与其他孩子结点之间的连线。
3. 层次调整。以树的根结点为轴心，将整棵树顺时针旋转一定的角度，使之结构层次分明。（注意第一个孩子是结点的左孩子，兄弟转换过来的孩子是结点的右孩子）

2）森林转换为二叉树

1. 把每棵树转换为二叉树。
2. 第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子，用线连接起来。

3）二叉树转换为树

1. 加线。若某结点X的左孩子结点存在，则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点…，都作为结点X的孩子。将结点X与这些右孩子结点用线连接起来。
2. 去线。删除原二叉树中所有结点与其右孩子结点的连线。
3. 层次调整。

4）二叉树转换为森林

假如一棵二叉树的根节点有右孩子，则这棵二叉树能够转换为森林，否则将转换为一棵树。

1. 从根节点开始，若右孩子存在，则把与右孩子结点的连线删除。再查看分离后的二叉树，若其根节点的右孩子存在，则连线删除…。直到所有这些根节点与右孩子的连线都删除为止。
2. 将每棵分离后的二叉树转换为树。

3、树和森林的遍历

1）树的遍历

分为两种方式

• 一种是先根遍历树，即先访问树的根结点，然后依次先根遍历棍的每棵子树。
• 另一种是后根遍历，即先依次后根遍历每棵子树，然后再访问根结点

2）森林的遍历

也分为两种方式:

• 前序遍历: 先访问森林中第一棵树的根结点，然后再依次先根遍历根的每棵子树，再依放用同样方式遍历除去第一棵树的剩余树构成的森林。
• 后序遍历: 是先访问森林中第一棵树，后根遍历的方式遍历每棵子树，然后再访问根结点，再依次同样方式遍历除去第一棵树的剩余树构成的森林。

森林的前序遍历和二叉树的前序遍历结果相同，森林的后序遍历和二叉树的中序遍历结果相同。

当以二叉链表作树的存储结构时，树的先根遍历和后根遍历完全可以借用二叉树的前序遍历和中序遍历的算法来实现。

四、二叉树的应用

1、BST（二叉排序树/二叉查找树/二叉搜索树）

1）定义

二叉排序树：又称为二叉查找树、二叉搜索树。它或者是一棵空树，或者是具有下列性质的二叉树。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值;
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值;
• 它的左、右子树也分别为二叉排序树。

二叉排序树利于插入和删除的实现。

2)操作

• 查找：查找成功返回ture，指向成功结点；查找失败返回false，指向上一结点。
• 插入：查找不成功，则插入到上一节点的子节点
• 构建：反复插入
• 删除：
  • 叶子节点直接删；
  • 只有左或右子树的，“子继父业”；
  • 左右子树都有的，找到需要删除的结点 p 的直接前驱(或直接后继) s，用 s 来替换结点 p，然后再删除此结点 s，s 的子结点移到 s 原来的位置

2、平衡二叉树

1）定义

• 平衡二叉树：是一种二叉排序树，其中每一个节点的左子树和右子树的高度之差的绝对值不超过 1。
• 平衡因子：二叉树上结点的左子树深度减去右子树深度的值（只可能是-1 、0 和 1）
• 最小失衡子树：在新插入的结点向上查找，以第一个平衡因子的绝对值超过1的结点为根的子树称为最小不平衡子树。

2）失衡调整

• LL失衡：右旋（Zig）。当传入一个二叉排序树 P，将它的左孩子结点定义为 L ，将 L 的右子树变成 P 的左子树，再将 P 改成 L 的右子树，最后将 L 替换 P 成为根结点。
• RR失衡：左旋（Zag）。与右旋对称。
• LR失衡：先左旋后右旋（Zig-zag）
• RL失衡：先右旋后左旋（Zag-zig）

3、堆

最大堆、最小堆

4、红黑树

把树中的节点定义为红、黑两种颜色，并通过规则确保从根节点到叶节点的最长路径的长度不超过最短路径的两倍。

5、哈夫曼(Huffman)树和哈夫曼编码

1）赫夫曼树定义

• 路径长度：从树中一个结点到另一个结点之间的分支构成两个结点之间的路径，路径上的分支数目称做路径长度。
• 树的路径长度：就是从树根到每一结点的路径长度之和。
• 带权路径长度：结点的带权的路径长度为从该结点到树根之间的路径长度与结点上权的乘积。
• 树的带权路径长度：为树中所有叶子结点的带权路径长度之和 。

赫夫曼树：带权路径长度 WPL 最小的二叉树称做赫夫曼树。

2)赫夫曼树构造

1. 根据给定的 n 个权值 {w_1,w_2,...,w_n} 构成 n 棵二叉树的集合 F={ T_1,T_2,...,T_n}，其中每棵二叉树 T_i 中只有一个带权为 w_i 根结点，其左右子树均为空。
2. 在 F 中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
3. 在 F 中删除这两棵树，同时将新得到的二叉树加入 F 中 。
4. 重复 2 和 3 步骤，直到 F 只含一棵树为止。这棵树便是赫夫曼树。

3)赫夫曼编码

赫夫曼编码：对需要编码的字符集，统计各个字符出现的次数或频率，作为权值，构造赫夫曼树。规定赫夫曼树的左分支代表0，右分支代表1，从根节点到叶子结点所经过的路径分支组成的 0 和 1 的序列便为该结点对应字符的编码。

• 定长编码：像 ASCII 编码
• 变长编码：单个编码的长度不一致，可以根据整体出现频率来调节
• 前缀码：所谓的前缀码，就是没有任何码字是其他码字的前缀

一、栈

1 基本概念

• 栈：是限定仅在表尾进行插入和删除操作的线性表。后进先出LIFO
  • 栈顶(top)：允许插入和删除的一端
  • 核底(bottom)：另一端
• 栈的引入简化了程序设计，使关注范围缩小，聚焦于要解决的问题核心。

2 栈的顺序存储结构 - 顺序栈

1）存储结构

栈是线性表的特例，栈的顺序存储是线性表顺序存储的简化。

• 栈底：数组0端
• top 变量：指示栈顶元素在数组中的位置，空栈-1

2）基本操作

• 进栈push：栈顶指针加一，新插元素赋值栈顶空间
• 出栈pop：栈顶指针减一，返回原栈顶

3）两栈共享空间

一个数组来存储两个具有相同数据类型的栈，数组两端为栈底，向中间靠拢。

通常都是当两个栈的空间需求有相反关系时，才使用这样的数据结构。

3 栈的链式存储结构 - 链栈

1）存储结构

• 栈顶：单链表的头部，替代头结点

2）基本操作

• 进栈push：当前栈顶元素赋值给新结点后继，新结点赋值给栈顶指针
• 出栈pop：栈顶指针下移，释放原栈顶结点

3）顺序栈与链栈对比

• 如元素变化不可预料，最好是用链栈；
• 如元素变化在可控范围内，使用顺序栈。

4 栈的应用

1）递归

编译器使用栈实现递归

2）四则运算表达式求值

• 中缀表达式：标准四则运算表达式，所有的运算符号都在两数字的中间
  • 9 + (3 - 1) * 3 + 10/2
• 逆波兰表示：一种不需要括号的后缀表达法，所有的符号都是在要运算数字的后面出现
  • 9 3 1-3 * + 10 2 / +

1. 将中缀表达式转化为后缀表达式(栈用来进出运算的符号)。

• 从左到右遍历中缀表达式的每一数字和符号，若是数字就输出，即成为后缀表达式的一部分
• 若是符号，则判断其与栈顶符号的优先级，是右括号或优先级低于栈顶符号（乘除优先加减）则栈顶元素依次出栈并输出，并将当前符号进栈
• 一直到最终输出后缀表达式为止。

2. 将后缀表达式进行运算得出结果(栈用来进出运算的数字)。

• 从左到右遍历表达式的每个数字和符号，遇到是数字就进栈；
• 遇到是符号，就将处于栈顶两个数字出拢，进行运算，运算结果进栈
• 一直到最终获得结果。

二、队列

1 基本概念

• 队列：是只允许在一端进行插入操作、而在另一端进行删除操作的线性表。先进先出FIFO
  • 队尾：允许插入的一端
  • 队头：允许删除的一端称

2 队列的顺序存储结构 - 循环队列

1）存储结构

• 循环队列：队列的头尾相接的顺序存储结构
• front 指针：头指针
• rear 指针：尾指针。若队列不空，指向队尾的下一个位置
• 标志变量 flag：标记队列是否满了

2）基本操作

• 入队EnQueue：判满，新元素给尾指针位置，尾指针后移
• 出队DeQueue：判空，返回对头元素，头指针后移

3 队列的链式存储结构 - 链队列

队列的链式存储结构，其实就是线性表的单链表，只不过它只能尾进头出而已，我们把它简称为链队列。

• front 指针：头指针。指向头结点。
• rear 指针：尾指针。指向终端结点。

2）基本操作

• 入队EnQueue：新结点赋值给原对尾结点后继，新结点设为队尾结点，尾指针指向新结点
• 出队DeQueue：头结点的后继结点出队，头结点的后继改为其后面的结点。若链表除头结点外只剩一个元素时， 则需将尾指针指向头结点

3）循环队列与链队列对比

• 在可以确定队列长度最大值的情况下，建议用循环队列
• 如果无法预估队列的长度时，则用链队列

4 队列的应用

键盘输入显示器输出

排队

一、线性表的定义和基本操作

1）定义

线性表：零个或多个数据元素的有序排列。

除第一个元素外，每个元素有且只有一个直接前驱元素；除最后一个元素外，每个元素有且只有一个直接后继元素。

2）基本操作

• InitList：初始化
• ListEmpty：判空
• ClearList：清空
• GetElem：取值
• LocateElem：定位
• Listlnsert：插入
• ListDelete：删除
• ListLength：长度

二、线性表的实现

1 顺序存储

1）定义

线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表的数据元素。

2）存储结构

一维数组，存取时间性能为O(1)，随机存取结构

• 存储空间的起始位置：数组 data 的存储位置
• 线性表的最大容量：数组长度 MaxSize
• 线性表的当前长度 : length

3）主要操作

• 取值O(1)：返回数组中指定下标的值。下标超限抛异常
• 插入O(n)：从最后一个元素到插入位置元素依次后移，插入，表长+1。位置或长度有问题抛异常或扩容。
• 删除O(n)：从删除位置到最后元素依次前移，表长-1。删除位置不合理抛异常。

4）优缺点

优点

• 无须为表示表中元素之间的逻辑关系而增加额外的存储空间
• 可以快速地存取表中任一位置的元素

缺点

• 插入和删除操作需要移动大量元素
• 当线性表长度变化较大时，难以确定存储空间的容量
• 造成存储空间的”碎片”

2 链式存储

2.1 单链表

1）定义

不考虑相邻，哪有空就存哪，让每个元素知道它下一个元素的位置

2）存储结构

链式结构中，除了要存数据元素信息外，还要存储它的后继元素的存储地址。

• 单链表：每个结点中只包含一个指针域，n 个结点链结成一个链表
• 结点：数据元素的存储映像，由数据域和指针域组成
  • 数据域：存储数据元素信息的域
  • 指针域：存储直接后继位置的域
• 头指针：（必要元素）指向链表中第一个结点的存储位置
• 头结点：（可选元素）为方便操作，可在第一个结点前附设一个头结点。
  • 头结点的数据域可以不存储任何信息，也可以存储如线性表的长度等附加信息。
  • 有了头节点，对第一结点前插入和删除第一结点，与其他结点的操作就统一了
• 线性链表的最后一个结点指针为“空”

3）主要操作

• 读取O(n)：从第一个节点遍历
• 插入、删除：遍历查找第i个元素O(n)，改变指针，插入和删除O(1)
  • 若不知道位置，与顺序存储结构没有优势。知道位置后，优势很大
  • 对于插入或删除数据越频繁的操作，单链表的效率优势就越是明显
• 整表创建：动态生成链表。从空表起，依次建立元素结点，插入链表。
  • 头插法：新结点插入到头结点与前一新元素之间。
  • 尾插法：记录尾结点，新结点插在终端结点后面
• 整表删除：便利每个节点，在内存中将它释放

4）单链表与顺序存储优缺点

• 时间性能
  • 查找
    • 顺序：o(1)
    • 单链表：O(n)
  • 插入和删除
    • 顺序：平均移动一半元素，O(n)
    • 单链表：找出位置后，O(1)
• 空间性能
  • 顺序：需预分配，大了浪费，小了溢出
  • 单链表：无需分配不受限
• 若线性表需要频繁查找，很少进行插入和删除操作时，宜采用顺序存储结构。
• 若需要频繁插入和删除时，宜采用单链表结构。
• 元素个数变化较大或未知时，最好用单链表。
• 如长度确定，顺序存储结构效率会高很多。

2.2 静态链表

1）定义

针对没有指针的语言，用数组来代替指针描述链表，被称为静态链表。

2）存储结构

游标实现法：数组的元素都是由两个数据域组成， data 和 cur

• 数据域data ：用来存放数据元素
• 游标 cur ：相当于单链表中的 next 指针，存放该元素的后继在数组中的下标
• 第一个元素：存放备用链表的第一个结点的下标
• 最后一个元素：存放第一个有数值的元素的下标

3）主要操作

将可用空间链成备用链表

• 插入
  • 模拟空间分配：从备用链表上取第一个结点作为待插入的新结点
• 删除
  • 模拟空间释放：将删除位置加入备用链表第一位

4）静态链表优缺点

• 插入和删除操作时 ，只需要修改游标。
• 没有解决连镇存储分配带来的表长难以确定的问题
• 失去了顺序存储结构随机存取的特性

2.3 循环链表

1）定义

循环链表：将单链表中终端结点的指针端由空指针改为指向头结点，这种头尾相接的单链表称为单循环链表，简称循环链表。

2）差异

循环链表和单链表的主要差异就在于循环的判断条件上，原来是判断 p->next 是否为空，现在则是 p -> next 不等于头结点，则循环未结束。

3）尾指针

如用尾指针替代头指针，则查找开始结点和终端结点都很方便。

2.4 双向链表

1）定义

双向链表是在单链表的每个结点中，再设置一个指向其前驱结点的指针域。

2）主要操作

在插入和删除时，需要更改两个指针变量。顺序很重要，千万不能写反了。

• 插入
  • 先搞定插入结点的前驱和后继，再搞定后结点的前驱，最后解决前结点的后继。
• 删除
  • 将前结点的后继指向后结点，将后结点的前驱指向前结点

3 线性表的应用

队列和堆栈